Classroom Collaboration Supports Mathematical Generalizations

December 15, 2010

In mathematics classrooms, generalization is an important part of the curriculum.

When students know how to generalize they can identify commonality across cases, extend their reasoning beyond the range in which it originated, and derive broader results from particular cases. But generalization remains difficult for students to do, and for teachers to support.

UW-Madison education professor Amy Ellis studies the processes that support students’ productive generalizing in their math classrooms. She considers generalization a dynamic social process as well as an individual cognitive activity.

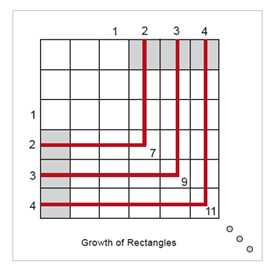
In a recent study she studied an 8th-grade math class during a 3-week unit on quadratic growth. The class sessions focused on relationships between the height and area of growing rectangles (see illustration). As they grew, the rectangles retained the same height-to-length ratio.

Ellis observed and catalogued all the actions that promoted students’ generalizations. These actions involved teachers, students, problems, and artifacts, all interacting with each other. As the 6 students and their teacher-researcher explored problems in quadratic growth, Ellis found patterns:  Students created and refined their generalizations through cyclical interactions. Each round of generalizing prompted the development of new generalizations. Here are the 6 activities that she found to support students’ generalizing:

• Publicly generalizing: when students create generalizations in a public manner, sharing ideas and results with others or generalizing out loud.
• Prompting a generalization: when a member of the class directly encourages a generalizing behavior on the part of another member.
• Publicly sharing: when a student shifts a generalization, or draws a solution or idea, from the private arena to the public arena for other students to consider, react to, and build from, by revoicing, requesting sharing, validating, or even rejecting.
• Encouraging reflection: when a student is asked to explain, clarify, justify, or prove a solution, pattern, or generalization. Clarifying actions request a clearer statement, explanation, or a re-statement of a generalization, solution, or idea.
• Building on an idea or generalization: when a student (or an artifact) builds on another student’s idea or conclusion.
• Focusing attention: when a teacher encourages students to attend to a specific feature of a problem, idea, or representation.

During this study the teacher-researcher repeatedly pressed the students to reflect on the generalizations they were developing—in particular, to explain why their strategies and ideas made sense. These reflection efforts, combined with the teacher-researcher’s revoicing acts, supported the students’ development of new generalizations. These efforts then provided the building blocks for students to refine and adjust their generalizations.

The teacher-researcher kept the group’s attention on each generalization or strategy by revoicing it and repeatedly encouraging students to reflect on its utility. This fostered an environment in which the students could refine their own ideas and build on one another’s work.

Ellis found, however, that the teacher is not the only one capable of providing leadership. Students who collaborate can also play this role. The act of making conjectures and generalizations public creates opportunities for students to respond to, accept or reject, reflect on, refine, and build on initial attempts. Students sift through ideas to pinpoint those that are mathematically powerful.

About This Study

The study took place at a public middle school in a mid-sized city. Participants were 8th-grade students who were enrolled in pre-algebra (3 students), algebra (2 students), or geometry (1 student). Two of the students were identified as high-achieving, 2 as medium, and 2 as low-achieving. There were 3 girls and 3 boys.