Measuring Coherence in Teacher Knowledge

September 2, 2014

To measure the coherence of teacher knowledge, researchers asked math teachers to react to a mathematical task. As teachers addressed the problem, patterns of connections among concepts became apparent. To visualize these patterns, the research team created conceptual “network maps” for each teacher. The stronger teachers invoked high numbers of concepts and demonstrated a clear pattern of connections among key concepts. The remaining teachers used fewer concepts or had fewer strong connections.

What does it mean for teachers to have coherent understanding of their subject?

Coherence is considered an important aspect of knowledge. Incoherent understanding of a subject reproduces disconnected facts. By contrast, coherent knowledge allows one to bring to a subject richly connected ideas, to zoom to the heart of a complex subject, and to offer strategic solutions. Yet coherence has seldom been defined or measured, even in the context of teaching and learning.

UW–Madison education professor David Williamson Shaffer and colleagues Chandra Hawley Orrill and James Burke, both at the University of Massachusetts Dartmouth, found a way to illustrate what coherence might mean in a teacher’s content knowledge.

Orrill’s pilot study was based on the Epistemic Frame Theory, developed at UW-Madison, which holds that not only do experts possess more knowledge than novices, their knowledge is organized in fundamentally different ways. Complex thinking can be understood in terms of the connections among “frame elements.”

Shaffer says one can think of expertise as a network of connections among specific understandings, articulated through discourse. For example, when asked to discuss a video of a complex teaching situation, expert teachers are better able to attend to important instructional aspects of the class, while novices are overwhelmed with details.

The research team used Epistemic Network Analysis (ENA) to uncover the connections teachers made among concepts. Assessing the development of expertise is a significant challenge, but ENA provides a way to quantify the relationships among ideas and thus to assess them. ENA focuses on the patterns of relations among discourse elements rather than individual ideas within that discourse. By treating epistemic frames as cognitive networks, different frame elements become “nodes” and the patterns of connections constitute the “links” among these nodes.

By quantifying these patterns of connections, ENA provides a way to measure complex thinking and problem solving. It’s a promising approach for exploring the question of what it means for a teacher to have more coherent understanding of his or her subject.

The Salad Dressing Recipe

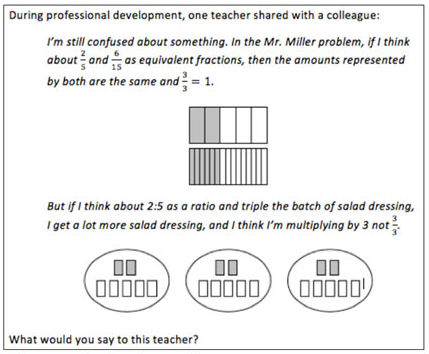
The researchers interviewed seven middle school mathematics teachers from both urban and rural school districts, whose experience ranged from one year to more than 10 years. They presented the teachers a mathematics task developed by Joanne Lobato that explored the relationship between fractions and ratios. The teachers applied different sets of skills, knowledge, and values to address the problem (see the salad dressing recipe in Figure 1).

After analyzing data from responses, the researchers created network maps for each teacher that reveal the ability to make connections among concepts. The maps differentiate the strong, middle, and weak teachers.

For strong teachers, thicker lines show node interactions occurring more than once (see Figure 2). They indicate areas of high coherence, defined as multiple connections. Teachers Greg and Lynda both had strong connections among discussing the fraction-ratio connection, discussing fraction operations, and interpreting the salad recipe problem. This suggests that they used general problem-solving skills. The second common area of high numbers of connections was the relationship between “attending to context” and “ratio-as-measure.”

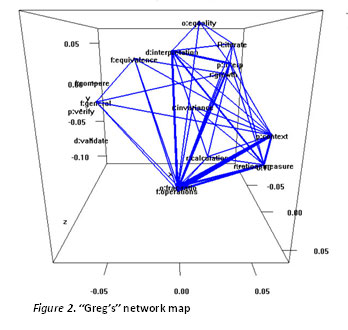
Like the strong teachers Greg and Linda, the middle teachers showed some patterns of connectedness among ideas, but they did not have as much balance between fraction and ratio ideas.

The weak teachers did not show a consistent pattern in terms of the number of connections. They made connections inconsistently. For example, Kate included a wide variety of concepts in her responses, but everything was connected evenly. Carrie introduced fewer concepts into her response to the task and there was no clear pattern of connectedness among her ideas.

Put another way, the strong teachers drew upon more concepts and made more connections among them. The middle teachers drew on fewer resources, yet they showed some connections among their ideas, suggesting coherence within those concepts. The weak teachers seemed to draw upon their resources without clear connections among the concepts they were studying.

This research moves beyond measuring the quantity of teacher knowledge to understandinghow teachers use their knowledge. By developing better understandings of knowledge coherence, researchers will be better able to support teacher development.